6 cách chứng minh tứ giác nội tiếp đơn giản, dễ hiểu

Chứng minh “Tứ giác nội tiếp” là một trong những dạng toán thông dụng của các bạn học sinh, các dạng toán này thường có trong các bài kiểm tra cũng như các kỳ thi quan trọng.

Để các bạn củng cố lại kiến thức, tự tin khi gặp phải các dạng toán này, INVERT đã tổng hợp được 6 cách chứng minh tứ giác nội tiếp trình bày dễ hiểu. Hãy chú ý theo dõi.

Những điều cần biết về tứ giác và tứ giác nội tiếp

Định nghĩa của tứ giác: Theo hình học phẳng Euclid, tứ giác là một đa giác hình gồm 4 cạnh và 4 đỉnh, trong đó không có bất kì 2 đoạn thẳng nào cùng nằm trên một đường thẳng. Tứ giác đơn có thể lồi hay lõm. Tổng các góc trong của tứ giác đơn ABCD bằng 360 độ.

Tứ giác nội tiếp: Một tứ giác có bốn đỉnh nằm trên một đường tròn thì được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp). Và đường tròn gọi là đường tròn ngoại tiếp, còn các đỉnh của tứ giác được gọi là đồng viên.

Định lý của tứ giác nội tiếp: Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180 độ. 

Định lý đảo: Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180 độ thì tứ giác đó nội tiếp được đường tròn

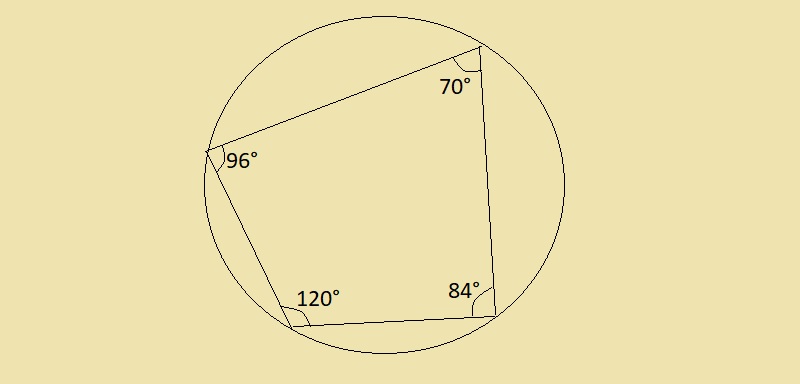
Hệ quả của tứ giác nội tiếp:

• Hai góc nội tiếp cùng chắn một cung thì bằng nhau.
• Góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung.
• Góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp cùng chắn một cung.

6 các cách chứng minh tứ giác nội tiếp 

Căn cứ vào định nghĩa, định lý cùng các dấu hiệu và hệ quả về tứ giác nội tiếp chúng tôi đã nêu ở trên . Dưới đây, là 6 cách chứng minh tứ giác nội tiếp đường tròn mà chúng tôi đã tổng hợp được. Cụ thể các cách đó như sau:

1/ Cách 1: Chứng minh tứ giác có tổng 2 góc đối bằng 180°

Chúng ta tiến hành chứng minh tứ giác có tổng hai góc đối bằng 180 độ là tứ giác nội tiếp: Từ định nghĩa của tứ giác nội tiếp ta có thể suy ra nội dung của phương pháp này như sau: “Nếu tứ giác ABCD có tổng hai góc đối bằng 180 độ thì tứ giác đó nội tiếp”.

Hệ quả của phương pháp này

Cho tứ giác ABCD:

• Nếu BAD = BCD = 90 độ thì tứ giác ABCD nội tiếp đường tròn tâm O, đường kính BD hoặc ACD = ABC = 90 độ thì tứ giác ABCD nội tiếp đường tròn tâm O, đường kính AC
• Nếu tổng hai góc kề bù EAD = BCD thì tứ giác ABCD nội tiếp đường tròn

Ví dụ: Cho tứ giác ABCD, chúng ta cần chứng minh ∠A + ∠C = 180° hoặc ∠B + ∠D = 180°, thì tứ giác ABCD là tứ giác nội tiếp đường tròn.

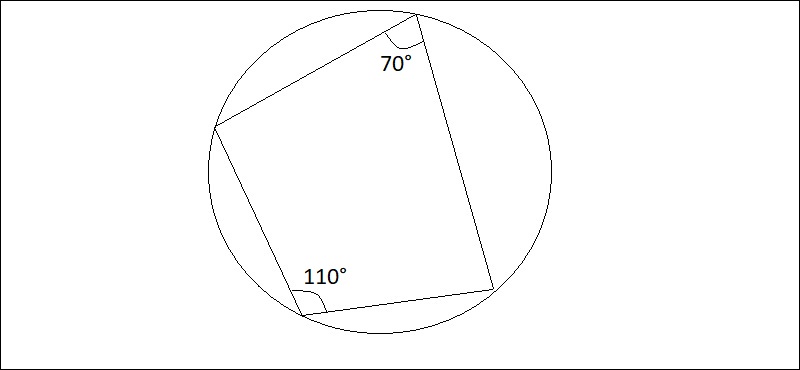
2/ Cách 2: Chứng minh qua góc ngoài của tứ giác

Chứng minh tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện là tứ giác nội tiếp

Ví dụ: Cho tứ giác ABCD, nếu chứng minh được góc ngoài tại đỉnh A bằng góc trong tại đỉnh C (tức là góc C của tứ giác đó) vì góc A và góc C đối đỉnh thì tứ giác ABCD nội tiếp đường tròn.

Đặc biệt ở cách làm này bạn phải chú ý vẽ đúng hình, đúng góc để có thể đưa ra kết quả đúng và tiếp tục làm các câu tiếp theo.

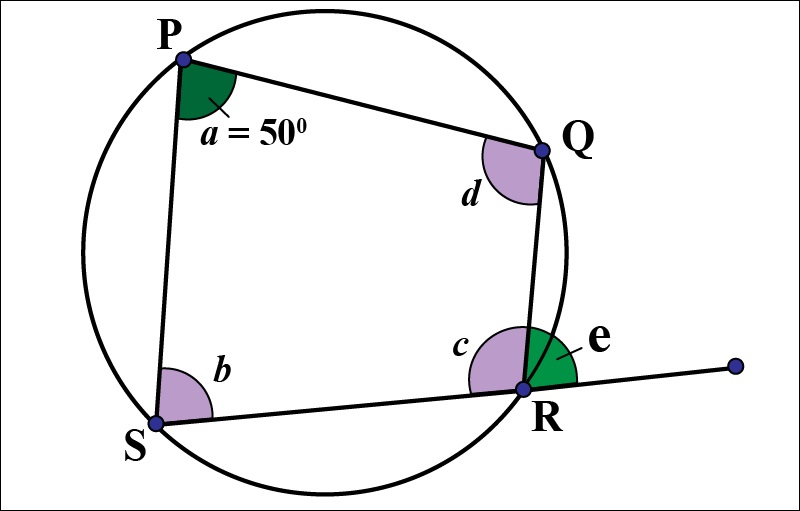
3/ Cách 3: Chứng minh từ hai đỉnh

Chứng minh hai đỉnh cùng kề một cạnh, cùng nhìn cạnh đó dưới hai góc bằng nhau và bằng 90 độ là tứ giác nội tiếp

Để chứng minh tứ giác ABCD trong phương pháp này nội tiếp, bạn cần đọc kỹ và chú ý đến dữ kiện đề bài đã đưa ra để chứng minh được rằng DAC = DBC = 90 độ và cùng nhìn cạnh DC. Từ đó bạn có thể suy ra tứ giác ABCD nội tiếp đường tròn. 

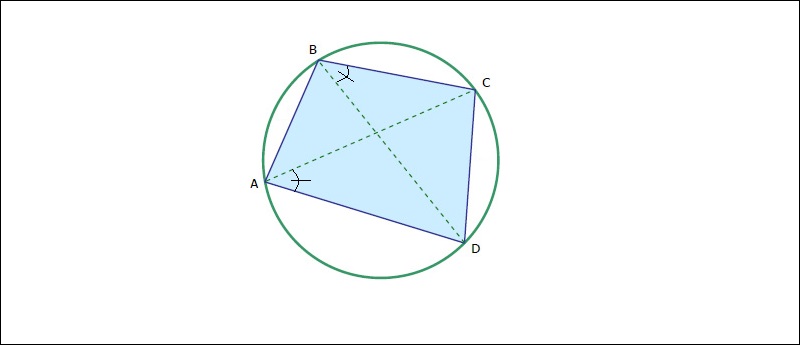
4/ Cách 4: Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó

Chứng minh bốn đỉnh của một tứ giác cách đều một điểm xác định là tứ giác nội tiếp

Khi đề bài cho trước tứ giác ABCD có đường tròn tâm O, bán kính R thì bất cứ điểm nào nằm trên đường tròn này đều cách tâm O một khoảng đúng bằng bán kính R. Dựa vào tính chất này, bạn có thể dễ dàng chứng minh tứ giác ABCD nội tiếp một đường tròn tâm O có bán kính R.

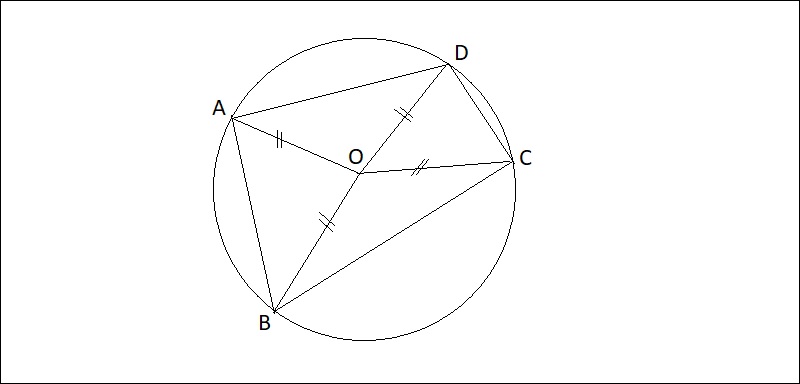
Ví dụ: Cho một điểm O cố định và tứ giác ABCD như hình minh hoạ bên dưới

Nếu các bạn chứng minh được điểm O cách đều 4 điểm A, B, C, D với khoảng cách bằng R, tức OA = OB = OC = OD = R thì điểm O chính là tâm đường tròn. Hay nói cách khác, có thể suy ra tứ giác ABCD nội tiếp đường tròn tâm O, bán kính R..

5/ Cách 5: Tứ giác có tổng số đo hai góc đối bằng nhau

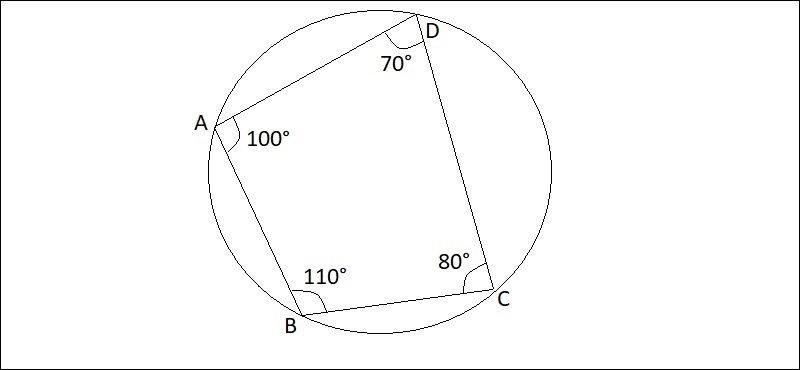
Chứng minh tứ giác có tổng số đo hai cặp góc đối diện bằng nhau là tứ giác nội tiếp

Phương pháp này chính là một trường hợp đặc biệt của phương pháp chứng minh thứ 2.

Ví dụ: Cho tứ giác ABCD và nếu chứng minh được tổng số đo hai góc: A + C = B + D thì có thể suy ra là tứ giác ABCD nội tiếp đường tròn. 

6/ Cách 6: Chứng minh bằng phương pháp phản chứng

Chứng minh dựa vào phương pháp phản chứng để có thể kết luận là tứ giác nội tiếp

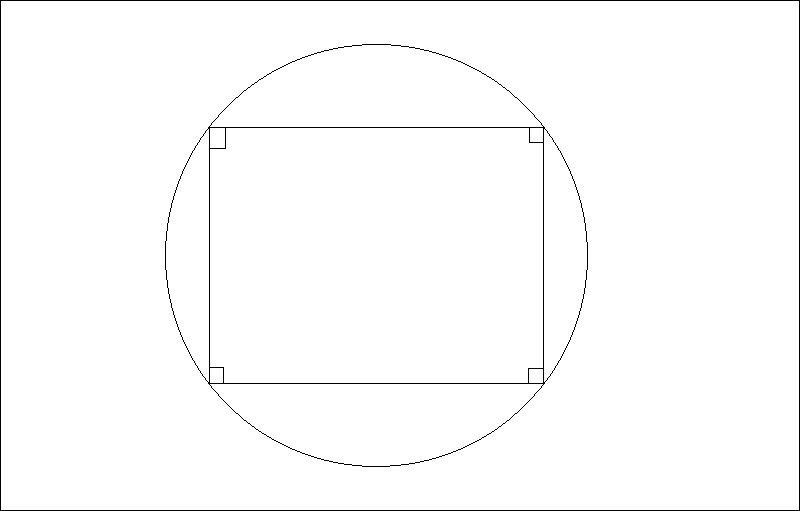
Bạn có thể chứng minh tứ giác ABCD được đề bài cho sẵn theo phương pháp này, thành một trong số các hình đặc biệt là hình thang cân, hình vuông và hình chữ nhật. Sau đó, dựa vào tính chất cơ bản của các hình này, dễ dàng suy ra tứ giác ABCD nội tiếp một đường tròn. 

Tóm lại, chúng ta chứng minh tứ giác ABCD là một trong những hình đặc biệt: Tứ giác ABCD là hình thang cân, hình chữ nhật hay hình vuông.

Một số lưu ý khi làm bài chứng minh tứ giác nội tiếp

• Các bạn nên vẽ hình to, rõ ràng, dễ nhìn và tránh vẽ hình tại một số trường hợp đặc biệt.
• Các kí hiệu góc, đoạn thẳng bằng nhau cần được đánh dấu rõ ràng hoặc có thể kí hiệu bằng bút khác màu để dễ nhìn hơn.
• Bám vào giả thiết đề bài đưa ra và áp dụng kiến thức đã học để làm bài cho hiệu quả.
• Những yêu cầu của đề bài cũng có thể là hướng gợi ý để giải quyết bài toán một cách dễ dàng.
• Không dùng những điều bạn đang cần chứng minh để chứng minh ngược lại chúng.

Bài viết trên đây là tất cả các cách mà chúng tôi tổng hợp được, giúp bạn chứng minh tứ giác nội tiếp một cách đơn giản, hiệu quả nhất, bạn có thể trang bị kiến thức cho bản thân, để có thể tự tin đối diện và vượt qua các bài kiểm tra với điểm số cao nhất.

Đăng ký theo dõi kênh Bất Động Sản Invert để nhận thông tin các dự án mới nhất.